Tools of Chaos

Orbits

September 28, 2022 · John Peach

Have you ever wondered why weather forecasts become less reliable the further into the future they try to predict? Or why the paths of planets and asteroids can sometimes behave in seemingly random ways? The answer lies in chaos theory - one of the most fascinating intersections of mathematics and natural phenomena.

In this article, we’ll explore the building blocks of chaos using the idea of orbits - the paths that objects or mathematical points take as they evolve over time. With computational tools available in the Julia language and some surprisingly simple equations, we’ll see how predictable rules can generate unpredictable behavior.

Concepts that we’ll cover in this article include:

By the end, you’ll have both an intuitive understanding of chaos theory and the practical tools to begin exploring it yourself. So let’s dive into the fascinating world where simple rules meet complex behavior.

Pluto Orbits

The previous post, Easy Chaos with Pluto showed how to run a Pluto notebook in Julia. A more in-depth introduction is on the MIT open course Introduction to Computational Thinking which describes the first-time setup of Julia and Pluto and provides a Cheatsheets page.

From JuliaDynamics we’ll use ChaosTools, DynamicalSystems, InteractiveDynamics, and DrWatson. You should also add DifferentialEquations, Plots, and GLMakie with Pkg, the Julia package manager.

Download the Pluto notebook, Orbits.jl used for this post.

The Discrete and the Continuous

In chaos theory, an orbit is the sequence generated by repeatedly applying a function ff to the initial point x0x_0.

S(x0)={x0,x1,x2,…}={x0,f(x0),f(f(x0)),…}S(x_0) = \{x_0,x_1,x_2, \ldots \} = \{x_0, f(x_0),f(f(x_0)), \ldots \}

Chaotic orbits may be either discrete or continuous. In the previous post Easy Chaos with Pluto the logistic function

xn+1=rxn(1−xn)x_{n+1} = rx_n(1-x_n)

is an example of a discrete system. For x0=0.2x_0 = 0.2 and r=4r = 4, this formula gives x1=0.64x_1 = 0.64. The sequence is {0.2,0.64,0.9216,0.289,…}\{0.2, 0.64, 0.9216, 0.289, \ldots \} which makes discrete steps between iterations.

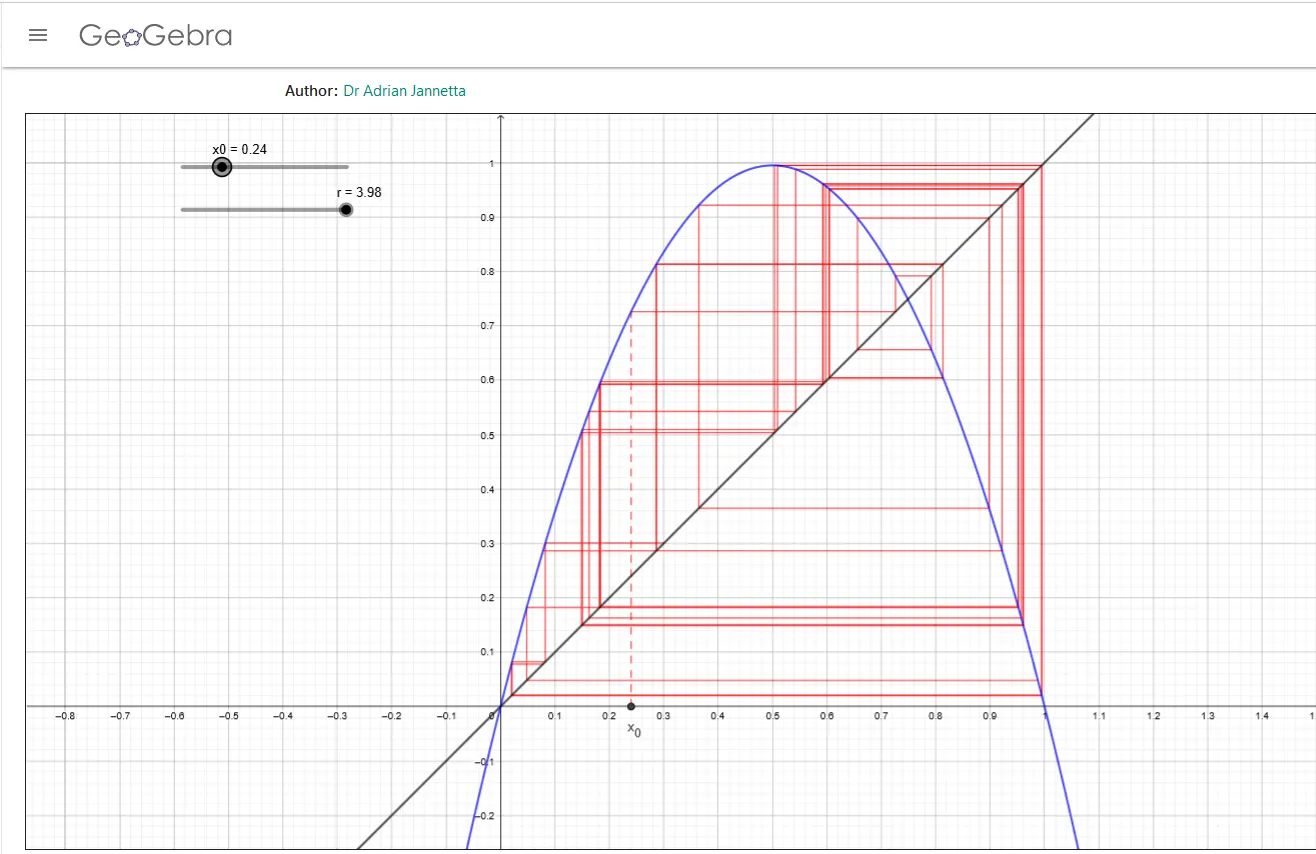
logistic-map-fixed-point-iteration
Figure 1.

Orbits of the logistic map in Geogebra.

Continuous functions are often written in terms of time, such as the Van der Pol equation

x˙=yy˙=μ(1−x2)y\begin{aligned} \dot{x} &= y \\ \dot{y} &= \mu (1-x^2) y \end{aligned}

Pick any point P=(x,y)P = (x,y). The notation x˙\dot{x} and y˙\dot{y} are the derivatives of xx and yy which tells you how fast point PP is moving. Suppose P=(1,3)P = (1,3). Putting those coordinates into the Van der Pol equation gives

x˙=3y˙=μ(1−12)×3=0\begin{aligned} \dot{x} &= 3 \\ \dot{y} &= \mu(1 - 1^2) \times 3 = 0 \end{aligned}

which says that the point PP is moving to the right with velocity 33, and the yy velocity is zero. The time variable tt doesn’t seem to show up, but (x˙,y˙(\dot{x},\dot{y}) is the velocity of PP which is a function of time. In some cases, you may see the notation x˙=dxdt\dot{x} = \frac{dx}{dt} or y˙=dydt\dot{y} = \frac{dy}{dt} indicating that velocities are functions of time. The ratio gives the slope mm of the velocity,

y˙x˙=dydt/dxdt.\frac{\dot{y}}{\dot{x}} = \frac{dy}{dt} / \frac{dx}{dt}.

Starting at point P0P_0, the velocity is v=(x˙,y˙)v = (\dot{x},\dot{y}), so for some small time step Δt\Delta t the next position would be P1=P0+Δt(x˙,y˙)P_1 = P_0 + \Delta t (\dot{x},\dot{y}). The time step can be as small as you like making the trajectory, or orbit, of P0P_0 a continuous function.

It isn’t too difficult to generate the sequence of points in the orbit of the logistic function, but for the Van der Pol equation the velocity changes with every small time step, so keeping track of the orbit points becomes tedious. Fortunately, computers can handle these kinds of equations and plot the orbits for us.

Chaotic Orbits

Orbits are chaotic if they have the following three properties:

One way to think about these properties is to imagine a car race. At the start they all have slightly different initial conditions. Some engines will be stronger than others, some drivers better than others, and only one car gets the pole position. Each car occupies a slightly different position on the track. These slight differences are the sensitive dependence on initial conditions that will determine the outcome of the race.

When the race starts the cars move down the track and begin to separate, each one completing laps at slightly different times than the others, and the paths that they take may be similar, but each car creates its own path. After enough time, the leaders will begin to lap the stragglers, and even though the cars separated at the start, they’re now back together, which is a little like topological transitivity.

The mathematical definition of topological transitivity says that for any two regions UU and VV in the orbit, there is some positive integer nn such that some of the iterated points in UU, or fn(U)f^n(U) can be found in VV. This holds no matter how small the regions UU and VV are, and no matter where they are in the orbit.

Not all of the points in UU will map into VV, and not all of the points in VV will be the result of iterated points in UU, but there will be at least one point that does map. Another way to think about this is that every point in the orbit approaches every other point through iterations of ff.

A consequence of topological transitivity is that an orbit is never two or more independent orbits. Even if the orbit appears to have distinct branches, eventually points in one branch will iterate into every other branch.

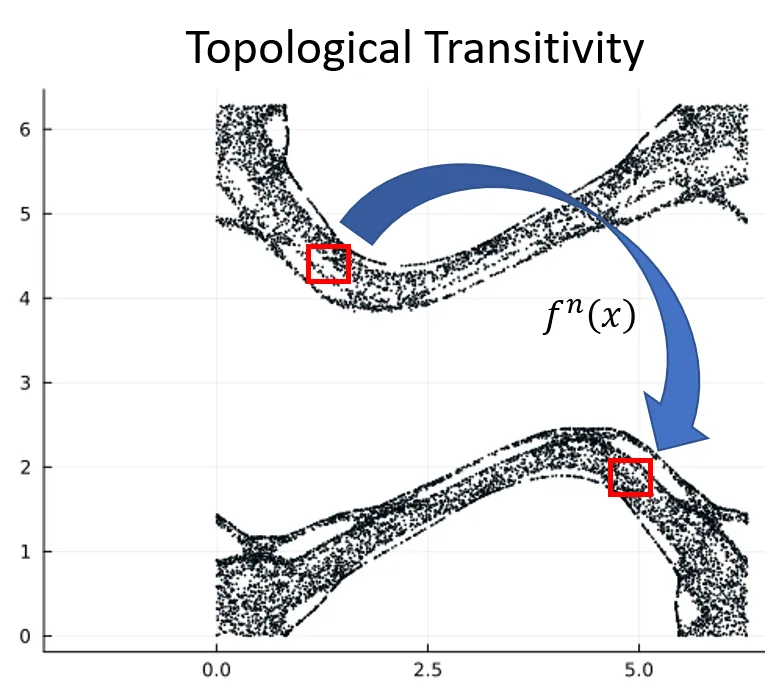
topological-transitivity
Figure 2.

Points in one orbit eventually map to points in every other branch.

A periodic orbit is one where fn(x0)=x0f^n(x_0) = x_0, so x0x_0 comes back to itself after nn iterations of ff. The cars go around the track and return to the points where they started. The analogy with race cars isn’t quite accurate because the lateral position on the track changes from lap to lap, but maybe you can imagine the propagation of points to be a little like a car race. Dense periodic orbits mean that at any point in the orbit of one point, you can always find the orbit of another point nearby.

These three properties of chaos were first described by Robert L. Devaney in his book, An Introduction to Chaotic Dynamical Systems. A popular non-mathematical book, Chaos: Making a New Science was published by James Gleick in 1987. Wolfram MathWorld says this about the definition of chaos,

Gleick notes that “No one [of the chaos scientists he interviewed] could quite agree on [a definition of] the word itself,” and so instead gives descriptions from a number of practitioners in the field. For example, he quotes Philip Holmes (apparently defining “chaotic”) as, “The complicated aperiodic attracting orbits of certain, usually low-dimensional dynamical systems.” Similarly, he quotes Bai-Lin Hao describing chaos (roughly) as “a kind of order without periodicity.”

Chaotic systems are deterministic which means there is no random component to an orbit. Given a starting position, in principle, you can calculate exactly where a point will be nn steps into the future for any value of nn. What makes them seem random is that two nearby starting points evolve in unpredictable ways.

The Orbits Notebook

The Orbits.jl notebook lets you experiment with both discrete and continuous dynamical systems using both built-in equations and systems you can write yourself. Using a built-in method is as simple as loading the dynamical system rule:

ds_henon = Systems.henon()

generating the trajectory

traj*henon = trajectory(ds*henon,100000)

and plotting the result

plot(traj*henon[:,1],traj*henon[:,2], seriestype = :scatter, aspect_ratio = :equal)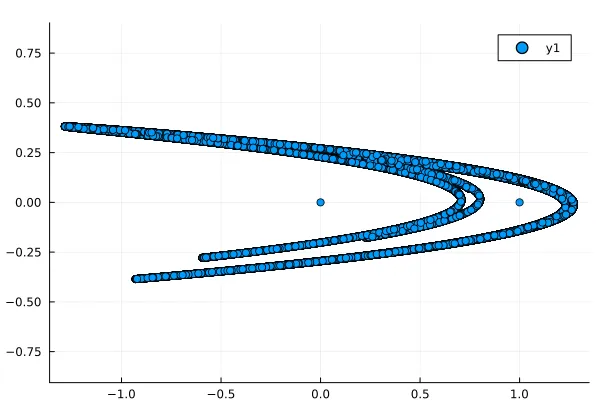
henon-map
Figure 3.

The Hénon Map.

The equations for the Hénon Map are

xn+1=1−αxn2+ynyn+1=βxn\begin{aligned} x_{n+1} &= 1 - \alpha x_n^2 + y_n \\ y_{n+1} &= \beta x_n \end{aligned}

which could have been written in Julia as

function henon_rule(u, p, n)
  x, y = u # Current state
  α, β = p # Parameters
  xn = 1 - α*x^2 + y
  yn = β*x
  return SVector(xn, yn)
end

After setting the initial condition uu and the parameter vector pp, we could generate the trajectory and plot it just as we did with the built-in version. The rule requires a step counter nn for discrete systems, or a time tt for continuous systems even if these variables don’t show up in the equations.

The Orbits.jl notebook is fully documented so you should be able to change parameters and extend equations or even create new systems. Have fun experimenting!

Taking Chaos Further

Throughout this article, we’ve explored how simple mathematical rules can generate surprisingly complex and unpredictable behavior. We’ve seen how chaos emerges from both discrete systems like the logistic map and continuous systems like the Van der Pol oscillator. The three key properties - sensitive dependence on initial conditions, topological transitivity, and dense periodic orbits - give us a framework for understanding what makes a system truly chaotic.

But this is just the beginning of what you can explore. Using the provided Pluto notebook, here are some other experiments you might try:

Hopefully, the tools and concepts we’ve covered here will allow you to continue the mathematical exploration of chaos. Whether you’re interested in weather patterns, population dynamics, or the motion of planets, chaos theory provides insights into the complex behavior of natural systems.

Code for this article

Orbits.jl - A Pluto notebook to study chaos

Software

References and further reading

Image credits

Hero: Iconic Arecibo Observatory’s 1000-feet telescope is beyond repair, will be demolished amid safety concerns Mihika Basu, MEAWW Nov 19, 2020.