The Big Squish Theory - Part II

Models, Mangles and Meshes

June 18, 2024 · John Peach

Baubles, bangles, hear how they jing, jinga-linga

Baubles, bangles, bright shiny beads

Sparkles, spangles, her heart will sing, singa-linga

Wearin’ baubles, bangles and beads

Computational Fluid Dynamics

Computational Fluid Dynamics (CFD) is used to model the motion of fluids. A volume of fluid is decomposed into many small cells where the physical properties of each cell can be calculated. The effects of actions on one cell are propagated to adjacent cells to determine the fluid flow. A numeric CFD solver can calculate pressures, temperatures, and fluid flows within a volume over very short time steps.

Recall from the previous post, The Big Squish Theory - Part I, that we tried to solve the Euler equations using the Wolfram Language, but found that the equations were too stiff.

Numerical solvers are often better able to handle stiff CFD problems. To solve the Euler equations numerically, we first need to create a grid, or stencil. In one direction are the steps in spatial dimension, Δx\Delta x, and the other direction are the time steps, Δt\Delta t.

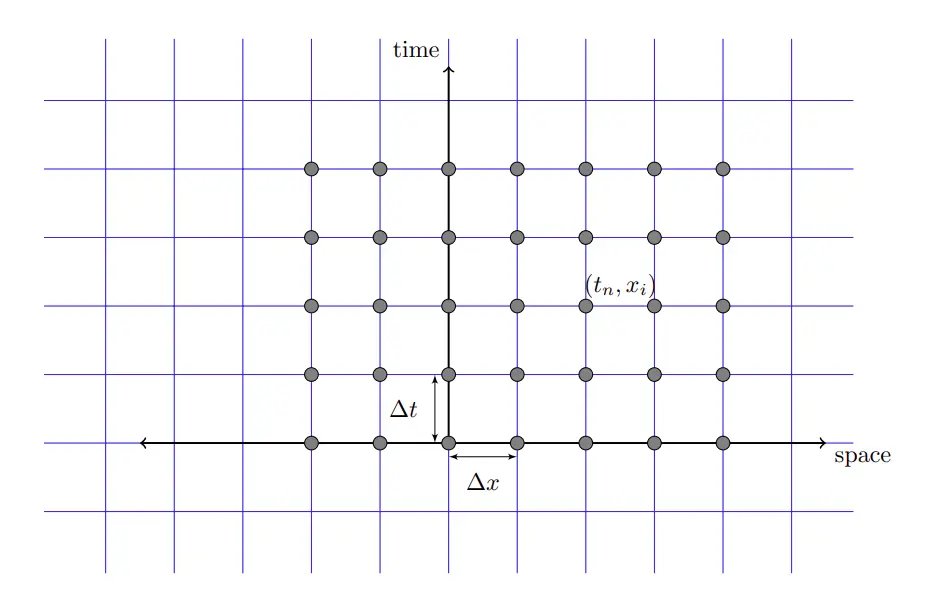
stencil
Figure 1.

CFD stencil.

Usually, numerical schemes calculate conditions by looking at the effects of nearby points in Δx\Delta x followed one by a time step forward. PDE solvers typically use a method-of-lines approach. This semi-discretizes the spatial derivatives, converting the PDE into a system of ODEs in time.

An appropriate time step size Δt\Delta t is then chosen to numerically integrate this ODE system, often using stability criteria like the Courant-Friedrichs-Lewy (CFL) condition,

C=uΔtΔxC = \frac{u \Delta t}{\Delta x}

where CC is the Courant number, and uu is the maximum velocity of the problem. The Courant number is a dimensionless number that measures how fast the solution is changing in space compared to how fast it is changing in time. A smaller Courant number means that the solution is changing more slowly in space, and therefore a larger time step can be used.

The time step in Euler’s is the left term

∂∂t(ρρvρE)\frac{\partial}{\partial t} \begin{pmatrix} \rho \\ \rho v \\ \rho E \end{pmatrix}

Computers work in discrete increments, so rather than calculating the instantaneous slope of each of these parameters ∂∂t\frac{\partial}{\partial t} we’ll have to use a small time step Δt\Delta t. Many methods for solving partial differential equations (PDEs) estimate conditions at several intermediate time steps and then combine the answers for conditions at the next time step.

We will also need to update conditions from nearby points using the second term

∂∂x(ρvρv2+p(ρE+p)v)\frac{\partial}{\partial x} \begin{pmatrix} \rho v \\ \rho v^2 + p \\ (\rho E + p) v \end{pmatrix}

that defines the rate of change of density, velocity, and specific energy. The spatial dimension is updated first because the fluxes, or changes in these parameters at the edges of the region depend on the solution at the current time step.

Once the spatial step has been chosen, the CFL condition can be used to calculate the maximum time step. The time step must be less than or equal to the maximum time step to ensure stability of the numerical solution.

In some cases, it may be necessary to use a smaller time step than the maximum time step to achieve the desired accuracy of the solution. This is often the case for problems with sharp features, such as shock waves.

Numerical solvers generally handle the time step part of the stencil but require the spatial coordinates as an input. For this, we need a way to build a model in 1,2, or 3 dimensions and a way to create a mesh on the model.

Models

Model Equations

Before you build the model, you should think about what problem you’re trying to solve and the PDE (partial differential equation) required. Some PDEs that can be solved on meshes are:

Coupling the heat equation with Navier-Stokes allows you to model flows of heated fluids. Some applications of PDE solvers are

Constructive Solid Geometry

Constructive Solid Geometry (CSG) is a technique used in solid modeling to represent solid 3D objects using Boolean operations on primitive shapes. Usually, the basic shapes consist of cubes, spheres, cylinders, and polyhedra combined using union, intersection, and difference operations. The Boolean operations are:

An example is this object derived from three cylinders, a cube, and a sphere:

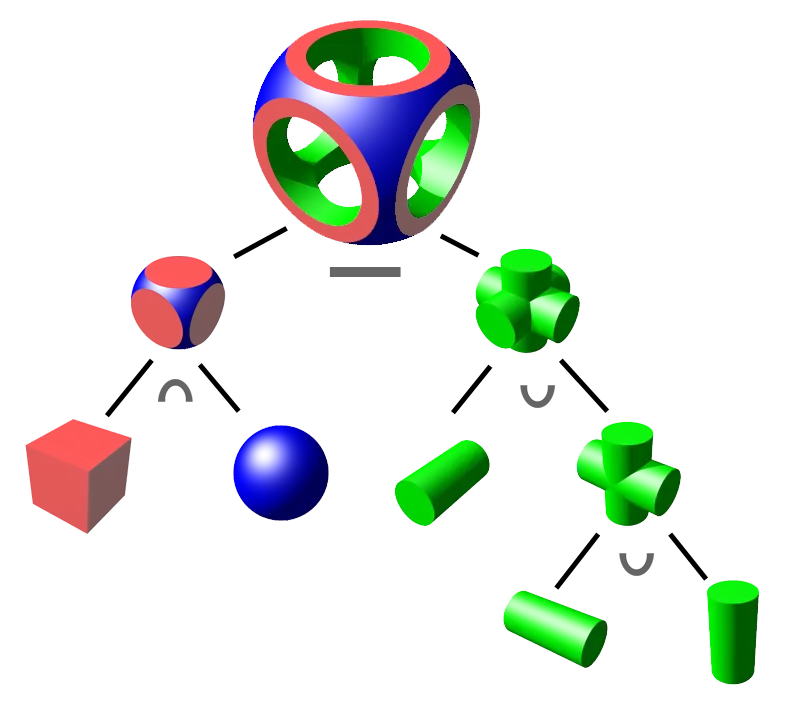
csg-tree
Figure 2.

Constructive solid geometry union and differences of a cube, sphere and cylinders.

CSG provides an intuitive way to model complex shapes using simple operations. Models are editable and parametric, but some shapes are difficult to represent. CSG models have trouble representing freeform sculpted surfaces.

A good place to get started with CSG is with OpenSCAD. The commands to build objects are pretty intuitive, so let’s try making the object shown above. The outline is called a tree, and the primitive objects at the ends of branches are called leaves.

On the left, two primitive objects, the cube and the sphere, are combined using an intersection operation to build the node above them. On the right, three cylinders are combined with a union operator after rotation to new orientations. Finally, taking the difference between the two new objects creates the finished form.

The OpenSCAD cheat sheet shows all of the possible basic shapes in 2D and 3D, as well as the Boolean operations, and possible transformations. A good way to get started is to build the cube on the left with: cube([1, 1, 1], center = true);. The x,y,zx,y,z dimensions are contained in the vector [1,1,1][1,1,1], and the command center = true puts the center of the cube at the origin. Note the semicolon at the end of the line. Press F5 to display the cube.

Since each side is length 11, then the distance from the center to the middle of any side is 12\frac{1}{2}, and the distance from the center to each corner is 32\frac{\sqrt{3}}{2}. If the radius of the sphere is less than 12\frac{1}{2} then the intersection with the cube leaves just the sphere, while if the radius is greater than 32\frac{\sqrt{3}}{2} the intersection leaves only the cube.

Spheres are automatically centered at the origin, and the command $fn=128 sets the number of facets used to represent the sphere since OpenSCAD can’t perfectly generate smooth rounded surfaces.

Here is the complete code to create the model.

// Shape parameters
sphereRadius = 0.65;
cylinderRadius = 0.3;
cylinderHeight = 1.1;

// Top-level difference operation
difference(){

    // Intersection of cube and sphere
    intersection(){
        
        // Red cube with unit sides
        color("red", 1.0){
            cube([1, 1, 1], center = true);
            }
        
        // Blue sphere 
        color("blue", 1){
            sphere(r = sphereRadius, $fn = 128);
            }
        }

    // Union of three cylinders centered on each axis
    color("Lime", 1.0){
        union(){
            union(){
                cylinder(h = cylinderHeight, r = cylinderRadius, $fn = 128, center = true);
                rotate([90,0,0]){
                cylinder(h = cylinderHeight, r = cylinderRadius, $fn = 128, center = true);
                }                
            }
            rotate([0,90,0]){
                cylinder(h = cylinderHeight, r = cylinderRadius, $fn = 128, center = true);
            }
        }
    }
}

The rendered model looks like this:

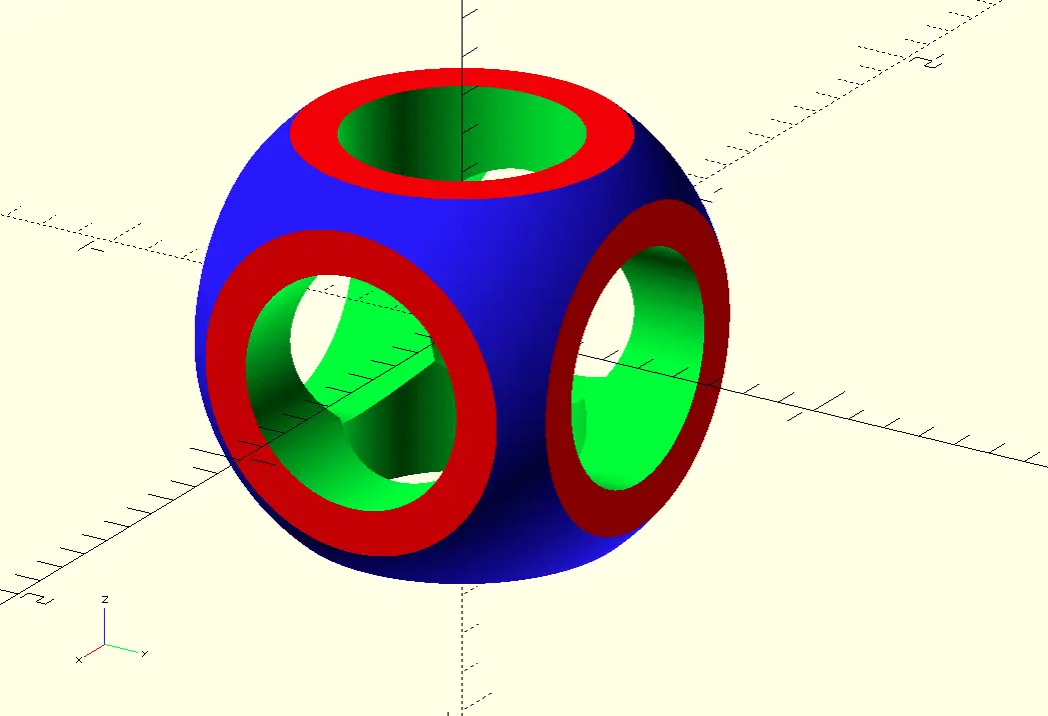
csg-object
Figure 3.

OpenSCAD model.

Other CAD (computer-aided design) systems can perform parametric modeling using Boolean logic on shapes, such as Open Cascade Technology (OCCT), FreeCAD, and Salome.

Mangles

Before we get into the details of mesh construction, there are times when the code used to construct the mesh creates an imperfect mesh. This can happen if the edges of adjacent cells don’t line up together, or if more than two faces connect to the same edge.

Fixing these problems can be tricky, and you’ll need software tools designed for these issues. Meshlab is very good at correcting mangled meshes, but may take a while to learn how to best fix the problems. For the BST the layout is simple so we won’t encounter any issues with the mesh. If the mesh is error-free, it is said to be “watertight”.

Meshes

Most meshes are formed from triangles or tetrahedra. A typical mesh looks like this,

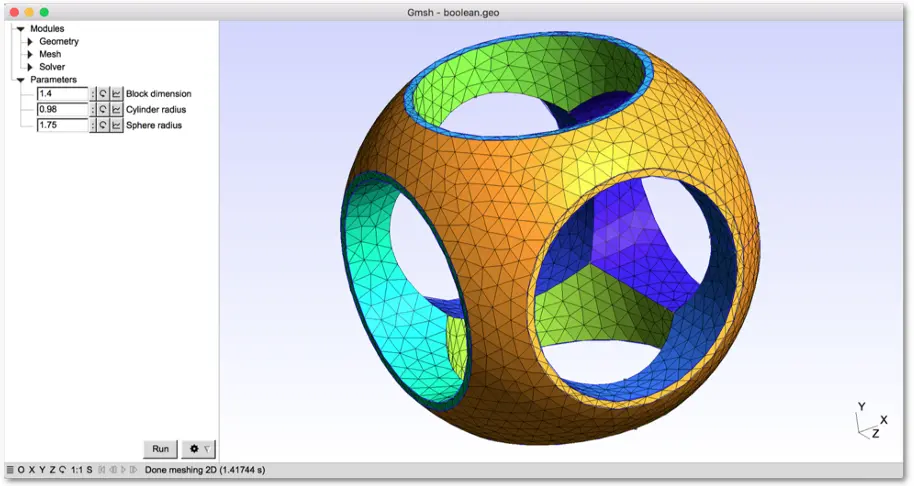
csg-mesh
Figure 4.

CSG mesh.

but for the BST problem, we only need to slice the box along the length to form a series of thin cells.

GMSH

Gmsh is a two or three-dimensional finite element mesh generator using Open Cascade Technology to generate models with constructive solid geometry. Download and install the latest version, and start Gmsh. For the Big Squish Theory simulation, any dimensions will do, but for the image below the dimensions are [−0.5,−0.05][-0.5, -0.05] for the location and [1,0.1][1, 0.1] for dxdx and dydy.

gmsh-box
Figure 5.

Gmsh shock tube.

To create each cell, we need to define the four vertices or points at the corners of the rectangle. Next, connect each pair of adjacent points with lines, then define a Line Loop that outlines the rectangle, and finally call the Line Loop a Surface.

Gmsh has a reserved term, Transfinite, which in mathematics means going beyond or surpassing any finite number, group, or magnitude. For Gmsh, this means that you can create or position lines, curves, surfaces, and volumes with non-integer values.

It sounds confusing, but it means that you can tell Gmsh that you want nn​ cells along the length of the rectangle, and it will figure out where to put the lines separating the cells, even if the locations are non-integer positions.

In Gmsh, the code to create the 2D shock tube for the Big Squish Theory is:

// Gmsh project created on Mon Jun 17, 2024
SetFactory("OpenCASCADE");

// Define points
L = 0.5;    // Tube length
H = 0.05;   // Tube width
N = 10;     // Number of rectangles along length of the tube
Point(1) = {0, 0, 0, 1.0};
Point(2) = {L, 0, 0, 1.0};
Point(3) = {L, H, 0, 1.0};
Point(4) = {0, H, 0, 1.0};

// Connect points with lines to form the rectangle
Line(1) = {1, 2};
Line(2) = {2, 3};
Line(3) = {3, 4};
Line(4) = {4, 1};

// Define the rectangle as a surface
Line Loop(5) = {1, 2, 3, 4};
Plane Surface(6) = {5};

// Define transfinite lines with a specific number of nodes
Transfinite Line {1,3} = N+1; // Adjust number for refinement in length of the tube
Transfinite Line {2,4} = 1;   // Adjust number for refinement in the width of the tube

// Define transfinite surface using the specified lines
Transfinite Surface {6} = {1,2,3,4};

// Recombine the surface mesh into quadrilaterals
Recombine Surface {6};

// Set the mesh element size
Mesh.CharacteristicLengthMax = 0.1;

// Generate the 2D mesh
Mesh 2;

// Save the mesh to a file
Save "shock_tube.msh";

In Gmsh click File →\rightarrow Open and select the file shock_tube.msh to view the mesh. A handy editor for Gmsh files is Notepad++.

Mesh Formats

Meshes come in many formats. We’ll give links to some of the standard formats, and show how to create a mesh from the locations of the vertices and the list of vertex links. Common mesh formats are:

Now go have some beer, bangers and mash. Next time we’ll run the Big Squish Theory simulation in SU2.

Irish-Bangers-and-Colcannon-Mash
Figure 6.

Bangers and Mash.

Code for this article

Software

Image credits