Red-Flag Day Geometry

Linear Algebra and Heron's Formula

September 27, 2024 · John Peach

We’re relaxing at the beach in Corolla, NC this week. It’s after Labor Day so prices are down and the crowds have left. The first couple of days were red-flagged meaning you can’t get in the water, but yesterday was fine and I got a boogie board and jumped in. But an offshore storm is developing and today is red-flag again. Even the birds don’t want to take off.

20240912_113509
Figure 1.

The dunes in Corolla, NC.

Luckily for me, I found this geometry problem to mess around with:

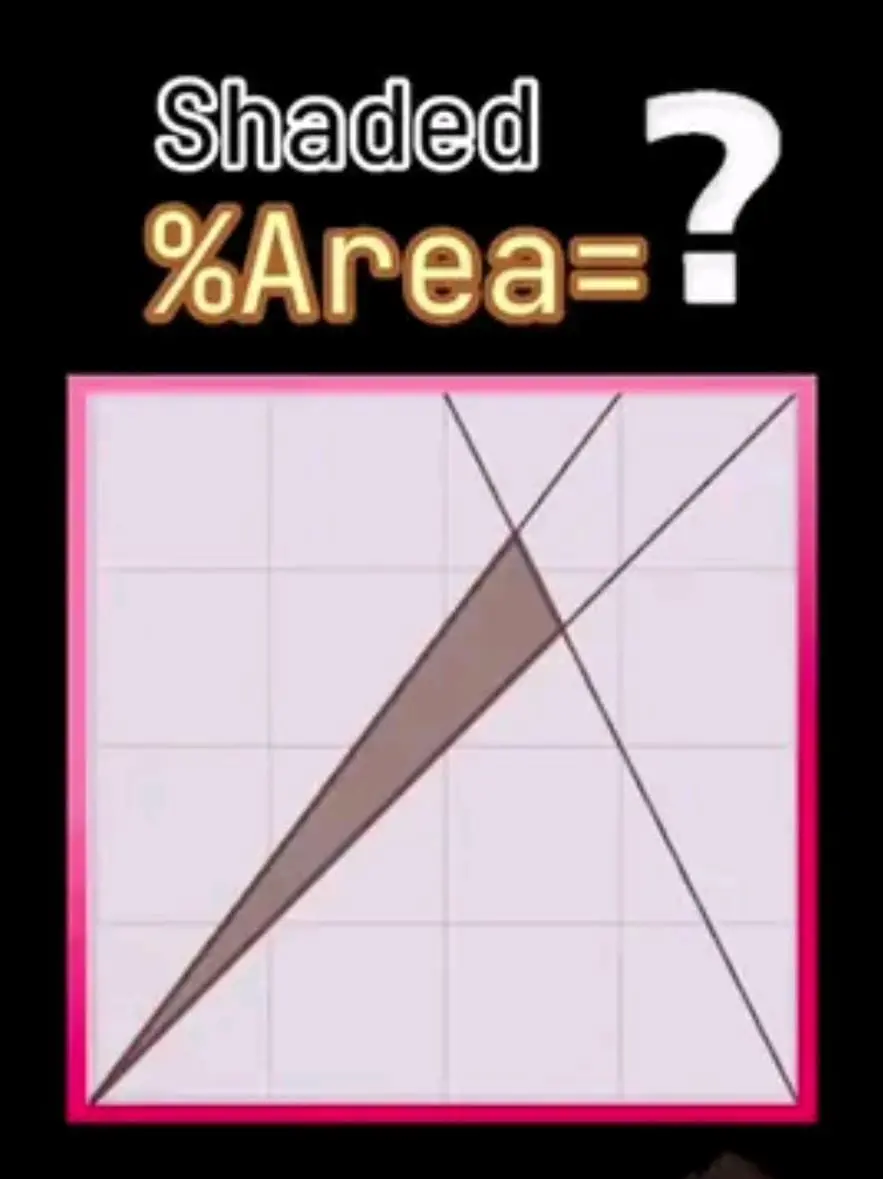
geometry-problem
Figure 2.

A geometry problem.

There are many ways to solve this, but I thought it might be interesting to try something a little different. Here’s the same problem in Geogebra:

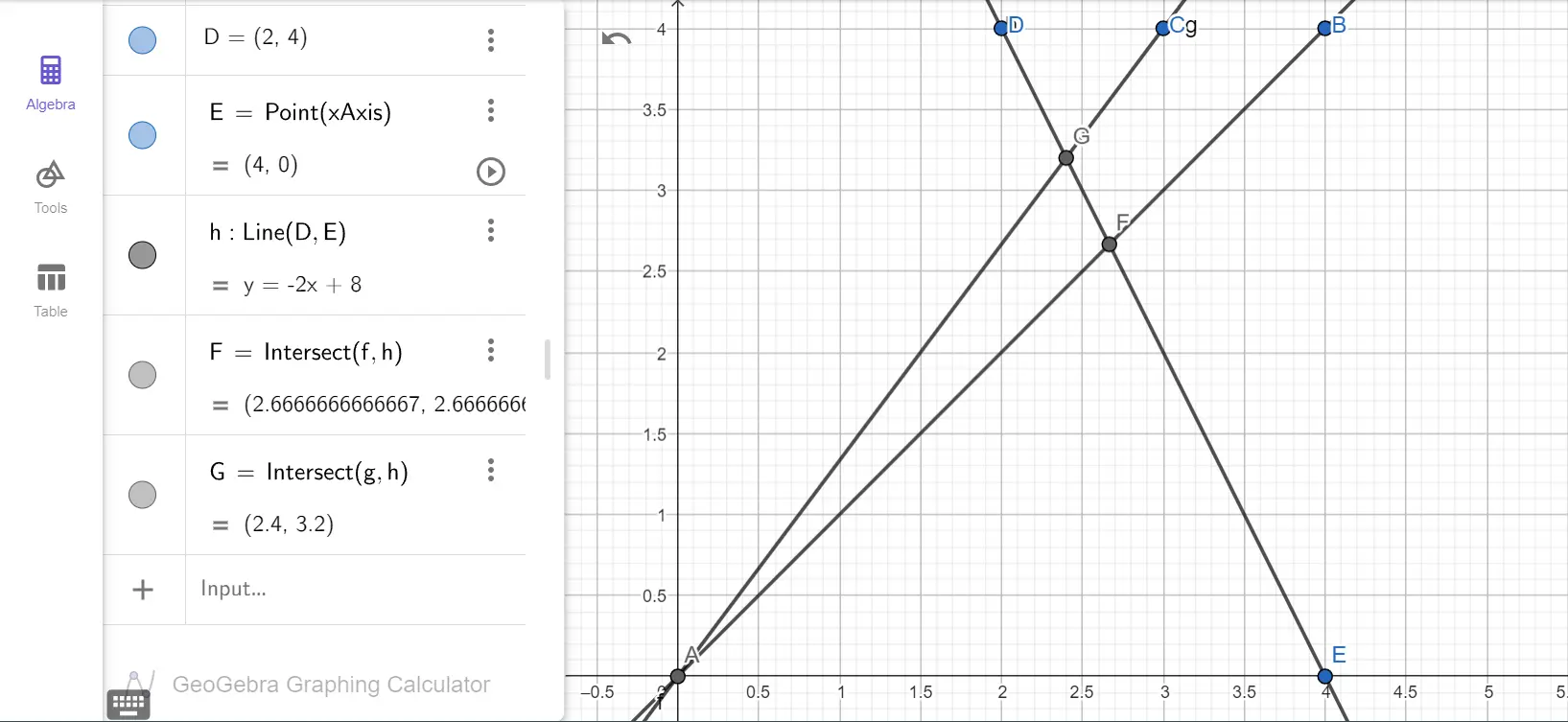
geogebra-image
Figure 3.

Geogebra line intersections.

The intersection of line ABAB and line DEDE is F=(83,83)F = (\frac{8}{3},\frac{8}{3}) and the intersection of ACAC with DEDE is G=125,165G = \frac{12}{5}, \frac{16}{5}. Geogebra does a great job of calculating the intersections, but there’s a nice trick for finding the intersection of two lines using linear algebra.

A linear algebra trick

Since two points define a line, we can start by looking at how pairs of points on two lines are related to the point of intersection.

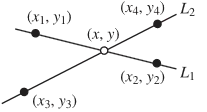
LineLineIntersection
Figure 4.

The point of intersection of two lines.

The equations of the lines L1L_1 and L2L_2 can be written in terms of their starting points (x1,y1)(x_1,y_1) and (x3,y3)(x_3,y_3), direction vectors, and coefficients uu and vv,

L1=[x1y1]+u[x2−x1y2−y1]L2=[x3y3]+v[x4−x3y4−y3].\begin{aligned} L_1 &= \begin{bmatrix} x_1 \\ y_1 \end{bmatrix} + u \begin{bmatrix} x_2 - x_1 \\ y_2 - y_1 \end{bmatrix} \\ L_2 &= \begin{bmatrix} x_3 \\ y_3 \end{bmatrix} + v \begin{bmatrix} x_4 - x_3 \\ y_4 - y_3 \end{bmatrix}. \end{aligned}

The point of intersection is then

(x,y)=(x1+u(x2−x1),y1+u(y2−y1))=(x3+v(x4−x3),y3+v(y4−y3)).\begin{aligned} (x,y) &= (x_1 + u(x_2-x_1), y_1 + u(y_2-y_1)) \\ &= (x_3 + v(x_4-x_3), y_3 + v(y_4-y_3)). \end{aligned}

If the intersection (x,y)(x,y) is between the points defining the lines then 0≤u,v≤10 \leq u,v \leq 1. But, how do we solve for uu and vv? Let’s rewrite the equations in vector form, letting the initial points be p=(x1,y1)p = (x_1,y_1) and r=(x3,y3)r = (x_3,y_3). Now,

L1=p+uqL2=r+vs\begin{aligned} L_1 &= p + uq \\ L_2 &= r + vs \end{aligned}

where the vector directions are q=[x2−x1y2−y1]q = \begin{bmatrix} x_2-x_1 & y_2 - y_1 \end{bmatrix} and s=[x4−x3y4−y3]s = \begin{bmatrix} x_4-x_3 & y_4 - y_3 \end{bmatrix}. For line L1L_1 the vector qq shows the direction you would need to go to get from the starting point (x1,y1)(x_1,y_1) to the ending point (x2,y2)(x_2,y_2).

The point of intersection (assuming the lines intersect) occurs when p+uq=r+vsp + uq = r + vs. Now here’s a neat trick - take the cross product of both sides with s,s,

(p+uq)×s=(r+vs)×s(p×s)+u(q×s)=(r×s)+v(s×s)(p×s)+u(q×s)=(r×s)\begin{aligned} &(p + uq) \times s = (r + vs) \times s \\ &(p \times s) + u(q \times s) = (r \times s) +v (s \times s) \\ &(p \times s) + u(q \times s) = (r \times s) \end{aligned}

since the cross product of any vector with itself is 00. Subtract p×sp \times s from both sides to get

u(q×s)=(r−p)×su (q \times s) = (r - p) \times s

and then solve for uu

u=∥(r−p)×s∥∥q×s∥.u = \frac{\Vert ( r - p ) \times s \Vert}{\Vert q \times s \Vert}.

You can solve for vv the same way,

v=∥(p−r)×q∥∥s×q∥v = \frac{\Vert ( p - r ) \times q \Vert}{\Vert s \times q \Vert}

but you only need one of the two solutions. The point of intersection is

Pint=p+uqP_{int} = p + uq

The cross product gives the angle between two vectors and is related to the lengths of each,

V1⃗×V2⃗=∥V1⃗∥∥V2⃗∥sin⁡(θ)V3⃗\vec{V_1} \times \vec{V_2} = \| \vec{V_1} \| \| \vec{V_2} \| \sin(\theta) \vec{V_3}

where the notation ∥V1⃗∥\| \vec{V_1} \| is the length of the vector V1⃗\vec{V_1} and θ\theta is the angle between vectors V1⃗\vec{V_1} and V2⃗\vec{V_2}. The direction of the cross product is V3⃗\vec{V_3} which is perpendicular to both V1⃗\vec{V_1} and V2⃗\vec{V_2}.

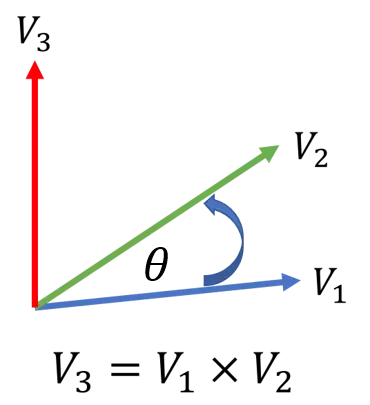
cross-product
Figure 5.

The cross product.

Testing the formula

We can test the formula by finding the intersection of the lines ABAB and DEDE. The line AB=L1AB = L_1 has initial point p=(0,0)p = (0,0) and direction q=(4,4)−(0,0)=(4,4)q = (4,4) - (0,0) = (4,4). The second line, DE=L2DE = L_2 has initial point r=(2,4)r = (2,4) and direction s=(4,0)−(2,4)=(2,−4)s = (4,0) - (2,4) = (2,-4). This gives

F=(83,83)F = \left( \frac{8}{3}, \frac{8}{3} \right)

as shown in the Geogebra plot. Call the function line_intersect in Julia as

p = [0;0];
q = [4;4];
r = [2;4];
s = [2;-4];
F = line_intersect(p,q,r,s)
2-element Vector{Float64}:
 2.6666666666666665
 2.6666666666666665

For the second intersection, change qq to [3,4][3,4] to get G=[2.4,3.2].G = \begin{bmatrix} 2.4, 3.2 \end{bmatrix}.

The inputs p,q,r,sp,q,r,s are all 2-element vectors, but the cross product requires 3-element vectors. This is corrected in the code by adding a 00 to the end of each input vector, e.g. push!(p,0). When the solution is calculated, the 3rd element is still there, so we use pop!(p_int) to remove the 00 in the z−z-direction.

Heron’s formula

You may know the formula for the area of a triangle as one-half the base times the height.

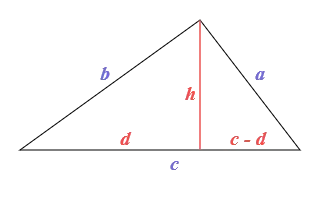
Triangle_with_notations_3
Figure 6.

A triangle with altitude hh splitting base cc into d+(c−d)d + (c-d).

The base is cc, but you have to calculate the height hh to get the area. Heron’s formula is more direct,

A=s(s−a)(s−b)(s−c)A = \sqrt{s(s-a)(s-b)(s-c)}

where ss is the semi-perimeter, or half the perimeter of the triangle,

s=12(a+b+c).s = \frac{1}{2}(a+b+c).

Heron of Alexandria (also known as Hero) was a mathematician and engineer

Hero_of_Alexandria
Figure 7.

Ἥρων, Heron of Alexandria.

Ἥρων, Heron of Alexandria

known for many inventions such as this steam engine called an aeolipile which uses the principle of action/reaction of steam venting through the pipes to spin the ball.

Aeolipile_illustration
Figure 8.

An aeolipile. Vented steam causes the ball to spin.

He is credited with the triangle area formula, but it was likely known much earlier.

There are many proofs of Heron’s formula such as this one which uses the Pythagorean formula for right angle triangles. In the figure above, we can get two representations of the altitude hh,

b2=h2+d2a2=h2+(c−d)2.\begin{aligned} b^2 &= h^2 + d^2 \\ a^2 &= h^2 + (c-d)^2. \end{aligned}

Subtracting the first from the second and solving for dd gives

a2−b2=(c−d)2−d2=c2−2cd+d2−d2=c2−2cdd=−a2+b2+c22c.\begin{aligned} a^2 - b^2 &= (c-d)^2 - d^2 \\ &= c^2 -2cd + d^2 - d^2 \\ &= c^2 - 2cd \\ d &= \frac{-a^2+b^2+c^2}{2c}. \end{aligned}

Substitute this value of dd back into the first Pythagorean formula and solve for hh to get

h2=b2−(−a2+b2+c22c)2=(2bc−a2+b2+c2)(2bc+a2−b2−c2)4c2=((b+c)2−a2)(a2−(b−c)2)4c2=(b+c−a)(b+c+a)(a+b−c)(a−b+c)4c2=4s(s−a)(s−b)(s−c)c2.\begin{aligned} h^2 &= b^2 - \left( \frac{-a^2+b^2+c^2}{2c} \right)^2 \\ &= \frac{(2bc - a^2 + b^2 + c^2)(2bc + a^2 - b^2 - c^2)}{4c^2} \\ &= \frac{((b+c)^2 - a^2)(a^2 - (b-c)^2)}{4c^2} \\ &= \frac{(b+c-a)(b+c+a)(a+b-c)(a-b+c)}{4c^2} \\ &= \frac{4s(s-a)(s-b)(s-c)}{c^2}. \end{aligned}

The first step above is to use the identity x2−y2=(x−y)(x+y)x^2 - y^2 = (x-y)(x+y), and then the third line is derived from (x±y)2=x2±2xy+y2(x \pm y)^2 = x^2 \pm 2xy + y^2.

Now that we have the height of the triangle we can get the area,

A=ch2=c24⋅4s(s−a)(s−b)(s−c)c2=s(s−a)(s−b)(s−c).\begin{aligned} A &= \frac{ch}{2} \\ &= \sqrt{ \frac{c^2}{4} \cdot \frac{4s(s-a)(s-b)(s-c)}{c^2}} \\ &= \sqrt{s(s-a)(s-b)(s-c)}. \end{aligned}

The Julia code for Heron’s formula is included in redflag.jl as herons.

The Red Flag Solution

With these two functions, we can now solve the problem. In Julia define the points

A = [0,0];
B = [4,4];
C = [3,4];
D = [2,4];
E = [4,0];

The points of intersection are

F = line_intersect(A,B,D,E-D)
2-element Vector{Float64}:
 2.6666666666666665
 2.6666666666666665
G = line_intersect(A,C,D,E-D)
2-element Vector{Float64}:
 2.4000000000000004
 3.2

and the area of the small triangle is

T = herons(A,F,G)
1.0666666666666644

The problem asked for the ratio of the triangle area to the square area as a percentage:

T/16 * 100
6.666666666666653

Sometimes you might like having a lazy day at the beach and not doing much more than solve a crossword puzzle. Solving this geometry puzzle is a bit like doing a crossword puzzle. There might not be a practical application for it, but you will find many opportunities to solve for the intersections of two lines, and knowing Heron’s formula can also be handy.

This solution using linear algebra and Heron’s formula isn’t the only way to find the answer, and it’s always a good idea to check your answer by solving the problem with several unique methods.

I’m not sure why anyone would spend time making sand castles when you could be solving a geometry problem.

sand_castle_problem
Figure 9.

Hero of the beach.

A Day at the Beach

This geometry puzzle allowed us to look at a method to calculate the intersection of two lines using techniques from linear algebra, and to calculate the area of a triangle with Heron’s method. There are many practical applications where you’ll need to find the intersection of two lines such as:

Heron’s also might find practical applications in

While our beach puzzle was purely recreational, the techniques we used are fundamental tools in many fields of science and engineering. Whether you’re designing video games, analyzing satellite data, or planning construction projects, understanding geometric intersections and area calculations is invaluable.

And here’s a picture of a Brazilian jasmine I found at the beach.

brazilian-jasmine
Figure 10.

Brazilian jasmine.

Code for this article

The two Julia functions, line_intersect and herons are in the file redflag.jl.

Software

References and further reading

Image credits