Roulette Physics

Let the good times roll!

August 28, 2025 · John Peach

The Eudaemons

In the late 1970s a group of physics grad students at UC Santa Cruz thought they might make their fortunes by exploiting a loophole in the rules for roulette. In their greed, casinos allow players to continue placing bets after the croupier has set the ball spinning around the wheel, but only while it remains on the outer rim of the wheel. This extra time to bet means that the casino rakes in many more bets, but the grad students realized that it also meant they could apply the laws of physics to predict where the ball would land.

By measuring the speeds of the ball and the wheel they were able to determine the most probable winning pockets, turning a house advantage into a significant player advantage. At the time, there were no laws preventing someone from using a device to make these predictions so the Eudaemons, as they called themselves, built small computers into their shoes that gave them the edge.

The name Eudaemons came from Greek mythology and referred to a type of benevolent spirit and later was adopted into Aristotelian ethics to mean a state of happiness and well-being, which the Eudaemons hoped to create through sharing their roulette winnings.

In the end, technical problems prevented them from beating the casinos, but they took some of the ideas from chaos theory to beat the stock market. In The Eudaemonic Pie, Thomas Bass tells the story of the Santa Cruz physics students attempts to predict the outcome of a game of roulette.

The wheel

Roulette wheels have pockets numbered 1-36 plus a 0 and an extra 00 on American wheels. Betting on a single number returns 35-1, but the two extra pockets mean the probability of selecting the winning pocket are 1 in 38, giving the casino a 5.26% edge on every play. For European roulette, the average casino take is 2.7%, but most casinos worldwide use the American layout.

Figure 1.

American layout roulette wheel.

To begin play the croupier spins the wheel in one direction and the ball in the opposite direction. The initial velocity of the ball is sufficient to keep it on the outer rim, and during this time bets may continue to be placed. The outer rim is toroidal so that the ball contacts the outer rim at only one point.

Figure 2.

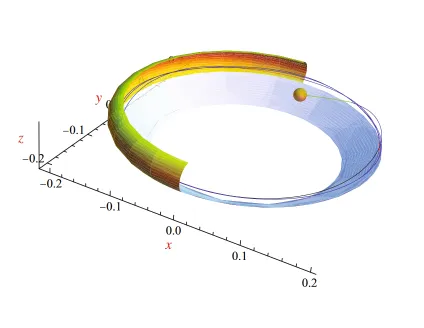
Ball path on the toroidal rim of the wheel.

After the ball slows sufficiently, it will leave the outer rim and begin to spiral towards the center of the wheel which is a shallow cone shape called the stator. The gold diamonds in each octant are raised to deflect the ball. Upon reaching the pockets, the ball may bounce and eventually land in some pocket other than the one initially entered.

Casinos make every effort to minimize wheel tilt, but a tilt as small as 0.2°0.2\degree is enough to affect the speed of the ball, causing it to increase velocity on the “downslope” side of the tilt, and slow on the other side.

Roulette Parameters

What are the physics that determine the pocket the ball falls into on the wheel? If you wanted to predict the winning pocket, what parameters would go into the equations? The first step in building a model is to consider a wide array of variables that determine the path, and then narrow the list to the ones that most heavily influence the outcome. A good list of potential variables helps to construct the model:

Equations of motion for the wheel

We’ll start by setting a fixed reference frame F0={i^,j^,k^}\mathcal{F}_0 = \{ \hat{i}, \hat{j}, \hat{k} \} where i^\hat{i} might be along the length of the table, j^\hat{j} is rotated 90°90\degree counterclockwise, and k^\hat{k} is up out of the table.

Figure 3.

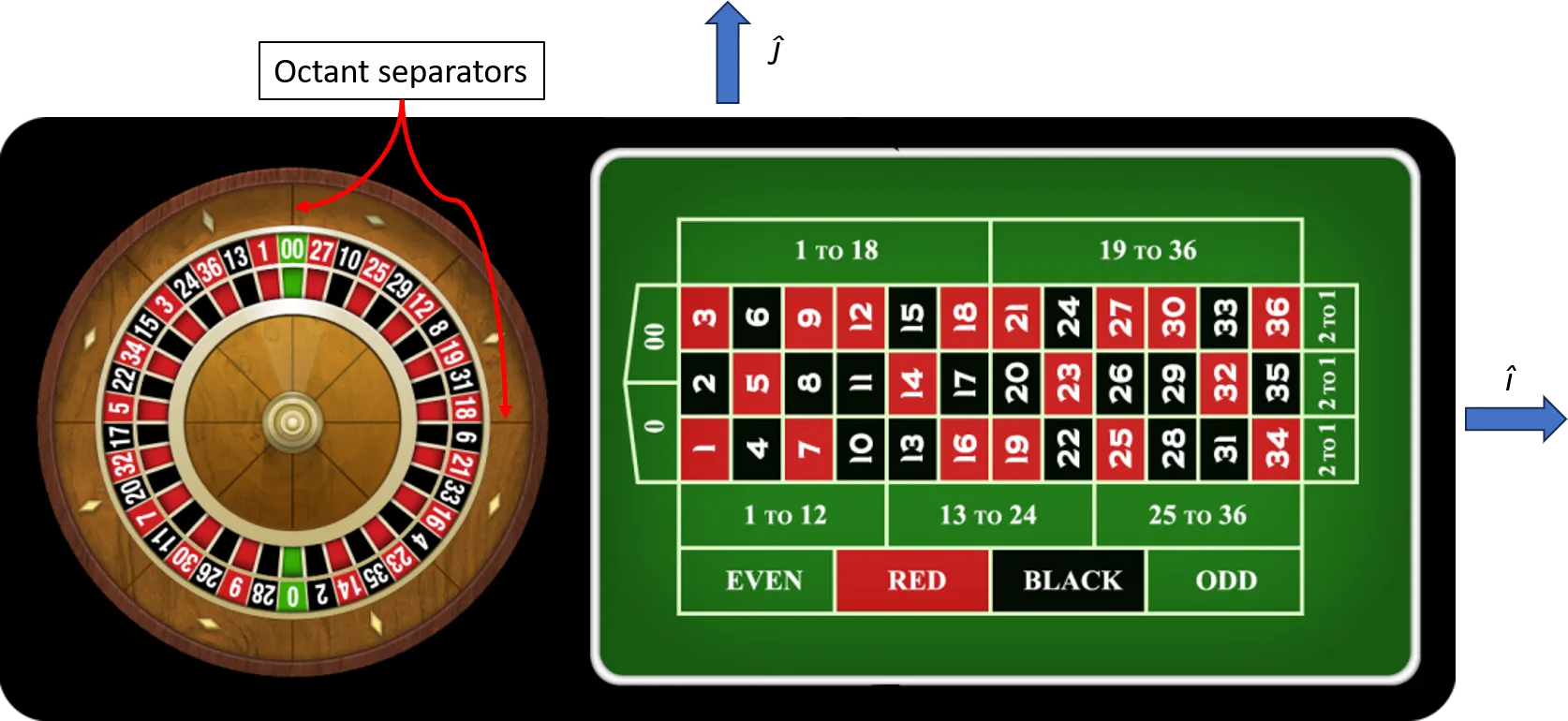
Roulette table and coordinate system.

Conveniently, the wheel is marked with lines separating the octants, and these lines can be used as references for the coordinate system. Parameters used to model the wheel are

An object with mass mm and velocity vv moving in a straight line has momentum p=mv  (kg⋅m/sec−1)p = mv \; (kg \cdot m/sec^{-1}) which provides a numerical value to express the effort required to bring the object to a stop. Similarly, the angular momentum of a roulette wheel measures how much force the croupier applied to get the wheel spinning.

For objects rotating with angular velocity ω\omega, the angular momentum is L=IωL = I \omega where II is the moment of inertia. The moment of inertia depends on both the mass of the object and its shape to account for how much mass is at each distance from the center of rotation.

For a roulette wheel, we can approximate the moment of inertia by assuming the wheel is a cylinder, so Iw=12MwR2I_w = \frac{1}{2} M_wR^2. The angular equivalent of force is torque which will slow the wheel’s rotation during play. The torque opposing the rotation is

M⃗=−cΩw(1)\vec{M} = -c \Omega_w \tag{1}

where cc is the damping coefficient (kg⋅m2/s)(kg \cdot m^2/s). The notation for the torque is M⃗\vec{M} (with an arrow) and shouldn’t be confused with the mass of the wheel MwM_w. For the wheel, angular momentum is

L⃗w=IwΩw.(2)\vec{L}_w = I_w \Omega_w. \tag{2}

For a linear system, force is equal to mass times acceleration, F=maF = ma, and acceleration is the rate of change of velocity, a=v˙a = \dot{v}. The wheel experiences torque due to friction which is the force slowing the rate of spin, Ω˙w\dot{\Omega}_w. Combining (1) and (2), torque is equal to moment of inertia times the change in angular velocity, so

M⃗=IwΩ˙w=−cΩw.(3)\vec{M} = I_w \dot{\Omega}_w = -c \Omega_w. \tag{3}

This can be rewritten as a first-order linear ordinary differential equation (ODE) in Ωw(t)\Omega_w(t)

Ω˙w+cIwΩ=0\dot{\Omega}_w + \frac{c}{I_w} \Omega = 0

with solution

Ωw(t)=Ω0e−t/τ where τ=Iwc,(4)\Omega_w(t) = \Omega_0 e^{-t/\tau} \text{ where } \tau = \frac{I_w}{c}, \tag{4}

and Ω0\Omega_0 is the initial angular velocity from the croupier’s spin. The wheel’s angular position Φw\Phi_w is the sum of the initial position Φw,0\Phi_{w,0} and the angular velocity integrated over time,

Φw(t)=Φw,0+∫0tΩ0e−s/τds=Φw,0+Ω0τ(1−e−t/τ).(5)\Phi_w(t) = \Phi_{w,0} + \int_0^t \Omega_0 e^{-s/\tau} ds = \Phi_{w,0} + \Omega_0 \tau \left( 1 - e^{-t/\tau} \right). \tag{5}

Motion of the ball

The ball experiences three phases as it transitions from initial spin to landing in one of the numbered pockets. During the first phase the speed of the ball is high and centripetal forces keep the ball on the outer rim. The second phase occurs when the speed reduces sufficiently that the ball begins spiraling inwards due to the slope of the wheel. Finally, the ball will hit a diamond shaped deflector which causes it to bounce. In some cases, the ball will return to the upper portion of the wheel and continue rolling until it encounters another deflector.

Phase I: Ball on outer rim

The radius of the wheel is RwR_w, and we’ll assume that the ball is a solid sphere with mass mm, and radius rr. Gravity acts in a downward direction (−k^),(-\hat{k}), and centrifugal force acts outward. The ball slows under the effects of rolling resistance and aerodynamic drag. The moment of inertia for a solid sphere is Ib=25mr2.I_b = \frac{2}{5}mr^2. The forces acting on the ball are:

The coefficient of rolling resistance μr\mu_r depends on the materials used to construct the ball and wheel, and surface roughness. For a roulette ball rolling on a wheel, μr≈0.002.\mu_r \approx 0.002.

The force due to aerodynamic drag depends on the coefficient of drag Cd=0.47C_d = 0.47 for a sphere, air density ρ,\rho, the cross sectional area of the ball A=πr2A = \pi r^2 and the forward velocity v.v. This equation for aerodynamic drag is valid for a sphere moving through a fluid without spinning, but works as a close approximation.

The ball rolls with angular velocity ωb=vr=Rwϕ˙b/r\omega_b = \frac{v}{r} = R_w \dot{\phi}_b / r where ϕ˙b\dot{\phi}_b is the angular velocity of the ball relative to the rim.

Figure 4.

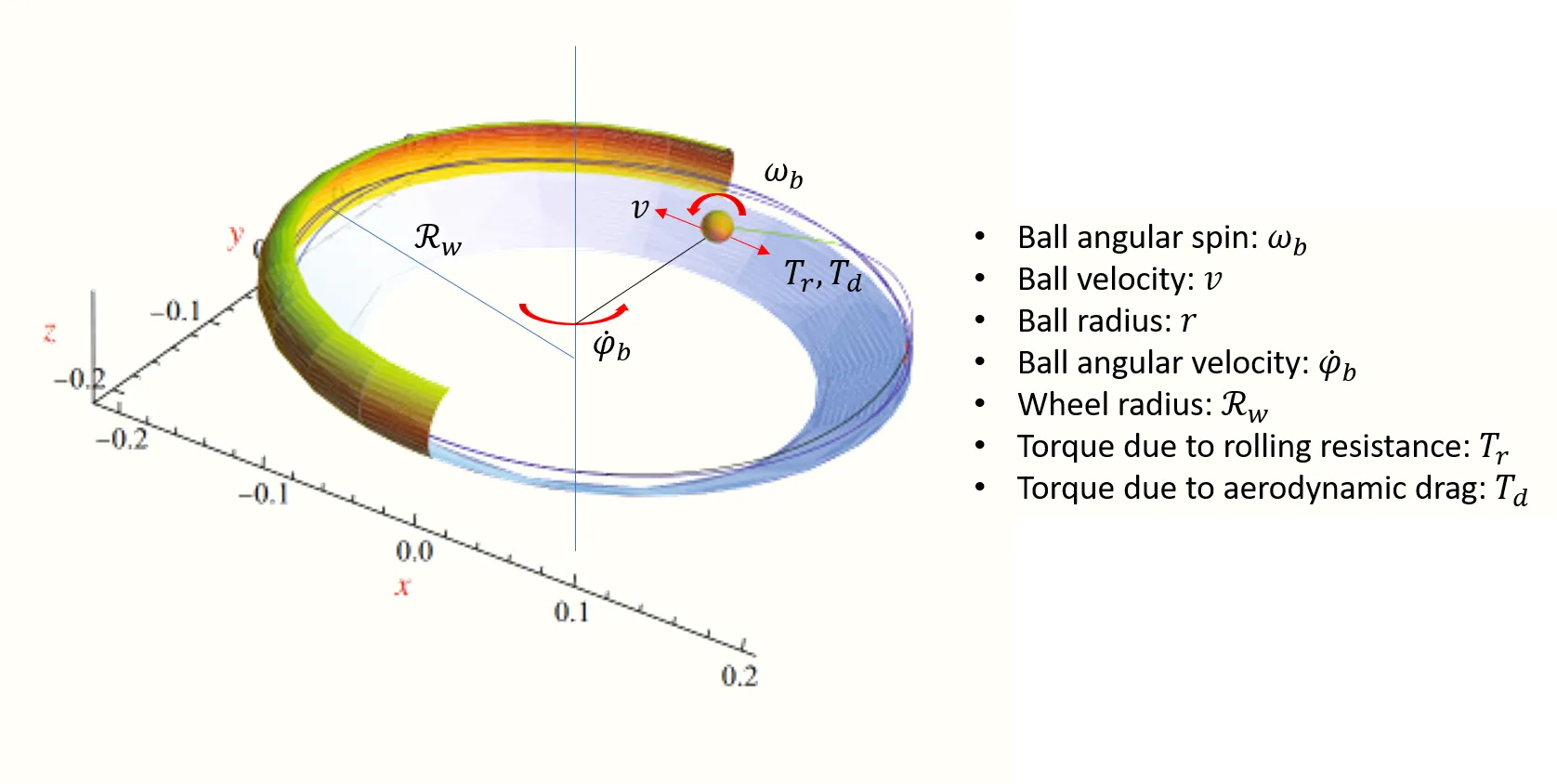
Parameters determining roulette physics.

The two torques (rolling and aerodynamic drag) act in the opposite direction to the ball velocity, and are applied at the center of the ball. Combined, they slow the rate of rotation, so

Ibωb˙=−Tr−Td.(6)I_b \dot{\omega_b} = -T_r - T_d. \tag{6}

Since ωb=Rwrϕ˙b\omega_b = \frac{R_w}{r} \dot{\phi}_b then (6) can be written as (ϕ¨\ddot{\phi} is angular acceleration)

IbRwrϕ¨b=−Tr−Td.(7)I_b \frac{R_w}{r} \ddot{\phi}_b = -T_r - T_d. \tag{7}

The torque TdT_d is due to the aerodynamic drag FdF_d applied at a distance rr, so

Td=rFd=12rCdρAv2=12rCdρARwϕ˙b2.(8)T_d = r F_d = \frac{1}{2} r C_d \rho A v^2 = \frac{1}{2} r C_d \rho A R_w \dot{\phi}_b^2. \tag{8}

Substituting for the moment of inertia IbI_b and rolling torque TrT_r in (7), (8) can be written as

ϕ¨b=−5μrg2Rw−5CdρA4mϕ˙b2.\ddot{\phi}_b = -\frac{5 \mu_r g}{2 R_w} - \frac{5 C_d \rho A}{4m} \dot{\phi}_b^2.

Letting A=5μrg2RwA = \frac{5 \mu_r g}{2 R_w} and B=5CdρA4mB = \frac{5 C_d \rho A}{4m} the ODE describing the ball motion on the outer rim is ϕ¨b=−A−Bϕ˙b2\ddot{\phi}_b = -A - B \dot{\phi}_b^2 with solution

ϕ(t)=ϕb(0)−1Blog⁡(cos⁡(AB(ϕ˙b(0)+t)))(9)\phi(t) = \phi_b(0) - \frac{1}{B} \log \left( \cos \left( \sqrt{AB} (\dot{\phi}_b(0) + t) \right) \right) \tag{9}

where ϕb(0)\phi_b(0) is the initial angle of the ball in the reference frame and ϕ˙b(0)\dot{\phi}_b(0) is the initial angular velocity.

The parameters in the first variable, AA, are the coefficient of rolling resistance μr\mu_r, gravitational acceleration gg and the wheel radius RwR_w. For the second variable, BB, the parameters are the aerodynamic coefficient of drag CdC_d, air density ρ\rho, frontal area of the ball AA, and the mass of the ball mm.

Phase II: Spiral descent on the conical wheel surface

The ball will leave the toroidal outer rim when the centrifugal force can’t overcome the gravitational force of the slope of the wheel. Assume the wheel cone slope is the angle α\alpha radians relative to the i^×j^\hat{i} \times \hat{j} plane. When

v2Rw<gcos⁡α\frac{v^2}{R_w} < g \cos \alpha

the ball will fall away from the outer rim, so Rwϕ˙b2<gcos⁡αR_w \dot{\phi}_b^2 < g \cos \alpha and we can define a critical angular velocity as

ϕ˙crit=gcos⁡αRw.(10)\dot{\phi}_{\text{crit}} = \sqrt{\frac{g \cos \alpha}{R_w}}. \tag{10}

This implies that the ball will always leave the rim at exactly the same angular velocity, irrespective of the initial velocity.

The ball now moves in a spiral trajectory on the cone of the wheel with polar coordinates (Rb(t),ϕb(t))(R_b(t), \phi_b(t)) where RbR_b is the radial distance from the wheel center to the ball. We can express the kinetic energy of the ball as

T=12m(R˙b2+Rb2ϕ˙b2sin⁡2α)+12Ibω2(11)T = \frac{1}{2}m \left( \dot{R}_b^2 + R_b^2 \dot{\phi}_b^2 \sin^2 \alpha \right) + \frac{1}{2}I_b \omega^2 \tag{11}

where the two components

Assuming the ball rolls on the wheel without slipping so so the translational speed divided by the ball radius gives the angular speed of the ball

ω=1rR˙b2+Rb2ϕ˙b2sin⁡2α\omega = \frac{1}{r}\sqrt{\dot{R}_b^2 + R_b^2 \dot{\phi}_b^2 \sin^2 \alpha}

giving

ω2=1r2(R˙b2+Rb2ϕ˙b2sin⁡2α).(12)\omega^2 = \frac{1}{r^2} \left( \dot{R}_b^2 + R_b^2 \dot{\phi}_b^2 \sin^2 \alpha \right). \tag{12}

The rotational kinetic energy is expressed in the second term of (11),

12Ibω2=12mr2⋅1r2(R˙b2+Rb2ϕ˙b2sin⁡2α)=15m(R˙b2+Rb2ϕ˙b2sin⁡2α).(13)\frac{1}{2}I_b \omega^2 = \frac{1}{2} mr^2 \cdot \frac{1}{r^2} \left( \dot{R}_b^2 + R_b^2 \dot{\phi}_b^2 \sin^2 \alpha \right) = \frac{1}{5} m \left( \dot{R}_b^2 + R_b^2 \dot{\phi}_b^2 \sin^2 \alpha \right). \tag{13}

Now, the total kinetic energy is the sum of the translational and rotational kinetic energy

T=Ttrans+Trot=12m(R˙b2+Rb2ϕ˙b2sin⁡2α)+15m(R˙b2+Rb2ϕ˙b2sin⁡2α)=710m(R˙b2+Rb2ϕ˙b2sin⁡2α).(14)\begin{aligned} T &= T_{\text{trans}} + T_{\text{rot}} \\ &= \frac{1}{2}m \left( \dot{R}_b^2 + R_b^2 \dot{\phi}_b^2 \sin^2 \alpha \right) + \frac{1}{5} m \left( \dot{R}_b^2 + R_b^2 \dot{\phi}_b^2 \sin^2 \alpha \right) \\ &= \frac{7}{10} m\left( \dot{R}_b^2 + R_b^2 \dot{\phi}_b^2 \sin^2 \alpha \right). \tag{14} \end{aligned}

The potential energy is the height of the ball times gravitational force mgmg, so

V=mgRbcos⁡α.(15)V = mg R_b \cos \alpha. \tag{15}

The Lagrangian is the difference between kinetic and potential energy, (see Lagrangian and Hamiltonian Mechanics in Under 20 Minutes)

L=T−V=710m(R˙b2+Rb2ϕ˙b2sin⁡2α)−mgRbcos⁡α.(16)\mathcal{L} = T - V = \frac{7}{10} m\left( \dot{R}_b^2 + R_b^2 \dot{\phi}_b^2 \sin^2 \alpha \right) - mg R_b \cos \alpha. \tag{16}

from which we can derive the Euler-Lagrange equations. For the radial component RbR_b,

∂L∂Rb=710m⋅2Rbϕ˙b2sin⁡α2−mgcos⁡α=75mR˙bddt(∂L∂Rb)=75mR¨b\begin{aligned} \frac{\partial \mathcal{L}}{\partial R_b} &= \frac{7}{10}m \cdot 2 R_b \dot{\phi}_b^2 \sin \alpha^2 - mg \cos \alpha = \frac{7}{5}m \dot{R}_b \\ \frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial R_b} \right) &= \frac{7}{5}m \ddot{R}_b \end{aligned}

so

75mR¨b=75mR˙bϕ˙b2sin⁡2α−mgcos⁡α\frac{7}{5}m \ddot{R}_b = \frac{7}{5}m \dot{R}_b \dot{\phi}_b^2 \sin^2 \alpha - mg \cos \alpha

or

R¨b=R˙bϕ˙b2sin⁡2α−57gcos⁡α(17)\ddot{R}_b = \dot{R}_b \dot{\phi}_b^2 \sin^2 \alpha - \frac{5}{7}g \cos \alpha \tag{17}

For the angular component, ∂L∂ϕb=0\frac{\partial \mathcal{L}}{\partial \phi_b} = 0 from conservation and

∂L∂ϕ˙b=75mRb2ϕ˙bsin⁡2α\frac{\partial \mathcal{L}}{\partial \dot{\phi}_b} = \frac{7}{5}m R_b^2 \dot{\phi}_b \sin^2 \alpha

so

ddt(∂L∂ϕ˙b)=75m(2RbR˙bϕ˙b+Rb2ϕ¨b)sin⁡2α.(18)\frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{\phi}_b} \right) = \frac{7}{5}m \left( 2 R_b \dot{R}_b \dot{\phi}_b + R_b^2 \ddot{\phi}_b \right) \sin^2 \alpha. \tag{18}

The Euler-Lagrange formulation says

ddt(Rb2ϕ˙b)=0⇒Rb2ϕ˙b=const=l.\frac{d}{dt}\left( R_b^2 \dot{\phi}_b \right) = 0 \Rarr R_b^2 \dot{\phi}_b = \text{const} = \mathcal{l}.

So angular momentum about the wheel axis is conserved,

ϕ˙b=lRb2(19)\dot{\phi}_b = \frac{\mathcal{l}}{R_b^2} \tag{19}

and substituting into (17)

R¨b=l2Rb3sin⁡2α−57gcos⁡α.(20)\ddot{R}_b = \frac{\mathcal{l^2}}{R_b^3} \sin^2 \alpha - \frac{5}{7}g \cos \alpha. \tag{20}

Rolling and Aerodynamic Drag

In the previous section we developed the Euler-Lagrange equations for the motion of the ball without including the effects of rolling friction and aerodynamic drag. The rolling resistance force opposes the direction of travel and is proportional to the mass of the ball and the coefficient of rolling friction,

Froll=−μrmgcos⁡α⋅sgn(R˙b).(21)F_{\text{roll}} = -\mu_r m g \cos \alpha \cdot \text{sgn}(\dot{R}_b). \tag{21}

While traveling on the conical part of the wheel, the ball’s speed is

∣v⃗∣2=R˙b2+Rb2ϕ˙b2sin⁡2α.(22)|\vec{v}|^2 = \dot{R}_b^2 + R_b^2 \dot{\phi}_b^2 \sin^2 \alpha. \tag{22}

Aerodynamic drag on the ball is approximately

F⃗drag=−12CdρA∣v⃗∣v⃗(23)\vec{F}_{drag} = - \frac{1}{2}C_d \rho A |\vec{v}| \vec{v} \tag{23}

where

The direction of the velocity vector v⃗\vec{v} rotates as the ball moves about the wheel, and the speed ∣v⃗∣|\vec{v}| (squared) can be written in polar coordinates as

∣v⃗∣2=R˙b2+Rb2ϕ˙b2sin⁡2α(24)|\vec{v}|^2 = \dot{R}_b^2 + R_b^2 \dot{\phi}_b^2 \sin^2 \alpha \tag{24}

so the drag force becomes

Fd=−12CdρAR˙b2+Rb2ϕ˙b2sin⁡2α  ⋅  R˙b.(25)F_d = -\frac{1}{2}C_d \rho A \sqrt{ \dot{R}_b^2 + R_b^2 \dot{\phi}_b^2 \sin^2 \alpha } \; \cdot \; \dot{R}_b. \tag{25}

Radial Equation of Motion

The total radial force (mass times radial acceleration) is

mR¨b=l2Rb3msin⁡2α−57mgcos⁡α−μrmgcos⁡α⋅sgn(R˙b)−kdR˙bR˙b2+l2Rb2sin⁡2α(26)\begin{aligned} m \ddot{R}_b &= \frac{l^2}{R_b^3} m \sin^2 \alpha - \frac{5}{7} m g \cos \alpha \\ &- \mu_r m g \cos \alpha \cdot \text{sgn}(\dot{R}_b) - k_d \dot{R}_b \sqrt{\dot{R}_b^2 + \frac{l^2}{R_b^2} \sin^2 \alpha} \tag{26} \end{aligned}

Dividing by the mass, mm,

R¨b=l2Rb3msin⁡2α−57gcos⁡α⋅sgn(R˙b)−μrgcos⁡α⋅sgn(R˙b)−kdmR˙bR˙b2+l2Rb2sin⁡2αϕ˙b=lRb2(27)\begin{aligned} \ddot{R}_b &= \frac{l^2}{R_b^3} m \sin^2 \alpha - \frac{5}{7} g \cos \alpha \cdot \text{sgn}(\dot{R}_b) \\ &- \mu_r g \cos \alpha \cdot \text{sgn}(\dot{R}_b) - \frac{k_d}{m} \dot{R}_b \sqrt{\dot{R}_b^2 + \frac{l^2}{R_b^2} \sin^2 \alpha} \\ \dot{\phi}_b &= \frac{l}{R_b^2} \end{aligned} \tag{27}

The variables used here are,

Wheel Tilt

Casinos routinely level the wheels because even a small amount of tilt can significantly alter the motion of the ball. The main effect is during the early stage when the ball is traveling on the outer rim.

Tilt causes the ball to speed up during part of the travel and slow down over the other half. Since the ball always leaves the rim at the same velocity, this means that sections of the rim become “forbidden zones” where the ball will remain attached.

Even a tilt of as little as 0.2°0.2 \degree creates a zone covering between a quarter and a third of the wheel where the ball will not leave the rim. By leveling the wheels, the tilt is generally kept to less than 0.6°0.6 \degree, but it is very difficult to achieve a perfect level.

Suppose the wheel has a tilt angle ϵ\epsilon relative to vertical, and the lowest point is an angle ϕ\phi from the i^\hat{i} axis. The angular displacement of the ball relative to the low point of the wheel is

θ(t)=ϕb(t)−ϕ.\theta(t) = \phi_b(t) - \phi.

The equation of motion of the ball traveling on the rim of a tilted wheel is

ϕb¨(t)=−αϕb˙(t)2+β−γsin⁡(ϕb(t)−ϕ)(28)\ddot{\phi_b}(t) = - \alpha \dot{\phi_b}(t)^2 + \beta - \gamma \sin(\phi_b(t) - \phi) \tag{28}

where

The ball exits the rim when centrifugal force falls below the effective gravitational component along the rim at that angular position. This happens when

ϕ˙b,f2=57gR(tan⁡δcos⁡ϵ−sin⁡ϵcos⁡(ϕb,f(t)−ϕ))(29)\dot{\phi}_{b,f}^2 = \frac{5}{7} \frac{g}{R} \left( \tan \delta \cos \epsilon - \sin \epsilon \cos (\phi_{b,f}(t) - \phi) \right) \tag{29}

where

Let the good times roll!

We now have a solid model of the motion of the ball on the wheel, and we know that the ball will always exit the rim at a known velocity. The spiral path of the ball towards the center is predictable until the ball hits one of the eight diamond deflectors. As Peter Gwynne says, “If you want to beat the house at roulette, it helps to think like a physicist.”

The Eudaemons couldn’t capitalize on their physics model for roulette due to equipment failures, but they found that small changes in differences in velocity, tilt, or drag could lead to dramatically different outcomes.

This sensitivity to initial conditions is the hallmark of chaos, but they were also able to detect and exploit patterns in the chaos. Their work highlighted how physical systems that appear random can, at least for a short time, be modeled and predicted using physics.

The equations we developed here are entirely deterministic and could be sufficient to improve the edge over the casino, but including chaotic effects would be an interesting next step.

A few questions remain that could improve the model:

Even with these questions unanswered, this is a great start for describing the physics of roulette.

Using a device to predict the outcome of roulette or any casino game is illegal in the United States. This article is intended to be an exploration of the physics of roulette, and not an endorsement to gamble.

Glossary

Angular momentum (LL) The rotational equivalent of linear momentum, equal to the moment of inertia times angular velocity (L=IωL = I\omega). It measures how much effort is required to change an object’s spin.

Angular velocity (ω\omega or Ω\Omega) The rate at which an object rotates, expressed in radians per second. For the roulette wheel, it is the spin rate.

Axis of rotation (nn) The straight line around which the wheel or ball spins.

Centripetal force The inward force needed to keep an object moving in a circular path. For the roulette ball, this keeps it pressed against the rim while it spins quickly.

Coefficient of drag (CdC_d) A dimensionless number describing how aerodynamic or streamlined an object is. A sphere has Cd≈0.47C_d \approx 0.47.

Coefficient of rolling resistance (μr\mu_r) A measure of how much rolling friction resists motion. For a roulette ball on the wheel, μr≈0.002\mu_r \approx 0.002.

Cone angle (α\alpha) The slope angle of the roulette wheel’s inner surface (stator). Determines how the ball spirals toward the center.

Critical angular velocity (ϕ˙crit\dot{\phi}_{\text{crit}}) The angular speed at which the ball can no longer remain on the rim and begins spiraling inward.

Euler–Lagrange equations Equations derived from the Lagrangian that describe the motion of a system. They are used to obtain the equations of motion for the ball on the roulette wheel.

Force (FF) A push or pull acting on an object, often written as mass times acceleration (F=maF = ma).

Inertia / Moment of inertia (II) A measure of how difficult it is to change an object’s rotation, depending on its mass and how that mass is distributed.

Lagrangian (L\mathcal{L}) A function defined as kinetic energy minus potential energy (L=T−V\mathcal{L} = T - V). It provides a convenient way to derive equations of motion.

Momentum (pp) The product of mass and velocity (p=mvp = mv). It describes how much motion an object has.

Potential energy (VV) Stored energy due to position. For the ball, it is the gravitational potential energy based on its height on the wheel’s slope.

Radial coordinate (RbR_b) The distance from the center of the wheel to the center of the ball.

Rolling resistance The resistive force opposing motion when a ball rolls along a surface. Caused by deformation and friction at the contact point.

Rotational kinetic energy The energy due to an object’s spin. For a solid sphere: 12Iω2\tfrac{1}{2} I\omega^2.

Solid sphere moment of inertia (IbI_b) For a solid ball of mass mm and radius rr, Ib=25mr2I_b = \tfrac{2}{5}mr^2.

Stator The shallow conical inner surface of the roulette wheel where the ball spirals inward after leaving the rim.

Torque (M⃗\vec{M}) The rotational equivalent of force. Torque causes changes in angular velocity.

Wheel tilt (ϵ\epsilon) A small deviation of the wheel’s axis from vertical. Even tilts as small as 0.2∘0.2^\circ can affect the ball’s path.

References and further reading

Image credits